How far is that anyway?
Skip to: What distance means | Measuring distance.
As Douglas Adams noted, "Space is big. Really big." But when it comes to actually putting numbers on things it starts to get complicated. Part of the problem is that the universe is expanding, so if something is a ten billion light years away, what does that mean? Is it that far away now, or was it that far away when the light was emitted, or something in between? Partly because of this there are different definitions of distance which are used by astronomers. In this guide, I'm only going to talk about the Luminosity Distance because that's what I quote in tweets, although I like to call it an effective distance because I think it's a more helpful name to people who don't deal with "luminosity" every day. And "effect. dist." makes for shorter tweets.

Image Credit: NASA/JPL-Caltech/vages/flickr
The other problem with distances is that how far away you think something is depends on the shape of the universe. The current consensus seems to be that space-time is shaped something like a 4-dimensional Pringle (see left, and nope, I can't picture it in 4-D either), but how tight the curves are etc is still an open question. You'll be glad to know I'm going to completely gloss over all of this issue by telling you from the off that any distances I quote take the assumption that the universe is Pringle-shaped, and 27% of the stuff in the universe is matter (most of which is probably dark matter, but that's another topic...).
This guide is therefore split into 2 parts. The first part, What distance means, explains what I mean by the "effective distance" and why that distance can be bigger than the universe(!). The second part Measuring distance, explains the concept of redshift which is the actual measurement which we have and the number that astronomers quote to each other when talking about distances.
What distance means
The measurement of distance which I quote in my tweets is technically called the luminosity distance but I will call it the effective distance because it is how far away the object effectively is, according to its brightness. More precisely, it's a measure of how much the light has spread out on its way to us.
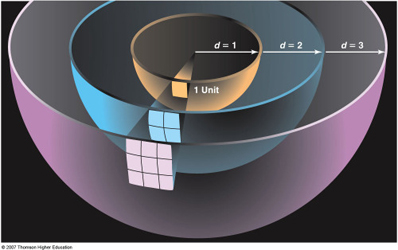
Image Credit: gain11.com
As you probably know, the further away you are from a light, the fainter it appears to you. In fact, if you double your distance from a light, it will look four times fainter. This is simply because the light is spread over a bigger area. The picture to the right demonstrates this. When you're looking at any light, you're actually a point on a sphere centred on the light. The light is spread evenly over the surface of that circle, which is just 4 × π × distance2. So when you move further away, the light you see was spread over the surface of a bigger sphere, and the surface area of that sphere has increased by the distance you moved, squared. This is called the inverse square law (because the intensity drops off as the 1/distance2) and crops up in a few areas of physics.
So when we talk about the luminosity distance or effective distance, what we really mean is the radius of a circle which has the distant object at the centre, that would make the object appear as bright as we see it. This is a really useful distance measure to have in astrophysics because it means if you know how bright the object looks, you can work out how bright it really was (just multiply it by the area of the circle you are on). This is why its proper name is luminosity distance: the brightness we measure is the flux but the actual brightness of the source is the luminosity, and to get from one to the other we need this luminosity distance.
Hang on though, the distance is bigger than the universe!
One of the problems with the luminosity distance is that you can end up with a number that just looks wrong. For example, the most distant object known to us (GRB 090423) has a luminosity distance of 323 billion light years, but the universe is only around 13 billion years old. But nothing can travel faster than light, so how did the object get so far away? This is one of those problems which comes from the universe being shaped like a Pringle. And expanding. Essentially the light has not gone in a straight line from the object to us, and space-time has been stretching whilst the light has been travelling. These mean that the light has apparently been spread out over a greater distance than you would intuitively expect.
There are other kinds of distance too. For example, the further away you are from something, the smaller it appears. So there's a type of distance measurement you can use not to work out how bright an object really is, but how big it really is. For more information about distances there is a wonderful short paper by David Hogg, and also some tutorials accompanying Ned Wright's Cosmology Calculator (the latter also lets you calculate different distances for different universe shapes and redshifts). These appear to be aimed more towards scientists than the general public, but are not too heavy.
Measuring distance
This is much more intuitive than what the distances mean. In fact, we don't measure distance. What astronomers measure is how fast something is moving, and thanks to Edwin Hubble (after whom the Hubble Space Telescope was named), we know that the faster something is moving, the further away it is from us. For a given shape of the universe, we can convert our measurement of speed into the luminosity distance (described above).
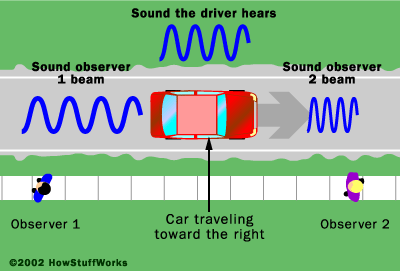
Image Credit: howstuffworks.com
So how do we measure speed? We use something called the redshift, which is really another name for the Doppler effect. This is a concept almost every child today is familiar with, even though they don't know it. When a child drives a toy car and makes a "neeeeeeooung" noise, they're reproducing the Doppler effect. Why does a car go "neeeeeeooung"? Because sound travels as waves. If a car is travelling towards you while giving off those sound waves then from your point of view the waves are being squashed together (which your ears interpret as a higher pitched sound). Or if the car is moving away from you, those waves are being spread out (a lower sound; see the image to the left). Another way of thinking about this is by imagining going to the beach*. You're standing knee-deep in the sea with a friend and, thanks to some odd weather, waves are hitting you once a second. A wave hits you and you start walking back to shore, while your friend stays still. A second later, your friend is hit by the next wave, but you are not - because you've moved. It takes a little longer for the wave to hit you. So you measure a bigger difference in time between the waves than your friend does. Conversely, if you'd started walking out to sea, the wave would have hit you first, so you'd measure a shorter time between waves.
The same is true of light, which can also be thought of as waves. When astronomers take a spectrum of an object (a bit like looking through a prism to make a rainbow, but in much more detail) they see some wavelengths (or colours) which are brighter or fainter than others (we call these spectral lines): these are caused by the chemical elements in the emitting or absorbing material. In a lab we can measure the wavelengths at which different chemicals produce lines. When we do this, and then compare those measurements to what we see from space, we can tell how much the wavelength has been changed, and so how fast the source of the light is moving towards or away from us.
In space, most objects are moving away from us, because the universe is expanding. This means that the light we see is stretched out - the wavelength is longer - and so the light appears redder. This is therefore called the redshift which is cryptically referred to with a lower case z. This is not a measure of distance, just of speed, but using a model of how we think the universe is expanding, we can convert the speed into a distance. Of course, as we learn more about the universe and refine our models, the conversion from redshift to distance may change so astronomers tend to talk in redshifts, not distances. And just to keep things complicated, the relationship between redshift and distance is not a simple, linear one. An object at z=2 is not twice as far away as an object t z=1. In fact, z=1 corresponds to about half way across the universe. At present the most distant objects known are galaxies, quasars (galaxies with massive gas-guzzling black holes at their centre) and GRBs. The most distant object ever seen (at least, that we know of, i.e. with a measured redshift) was GRB 090423, with z=8.3. There are other objects which people think, from their colour, may well be further away, but no useful spectrum exists for any of these objects, so we don't know for sure how far they are. But these things change! I'm sure the z=8.3 record will not last forever.
* This is a good solution for almost anything actually.